密码学基础笔记(三)

第9章 公钥密码学与RSA

保密性：信息不被泄露给未经授权者的特性。

公钥密码体制的基本原理

加密密钥≠解密密钥，加密密钥 ≠> 解密密钥，加密和解密变换分开实现。

  • 公开加密密钥（公钥）：任何人利用这个公钥和算法向该用户发送加密信息。
  • 保密解密密钥（私钥）：解密密文。

公钥密钥密码体制的优点是：

  • 不需要安全信道传递密钥，大大简化了密钥管理。
  • 实现了分组密码体制中无法实现的数字签名。

公钥密码体制

公钥密码体制的核心思想：加密和解密采用不同的密钥。这是公钥密码体制和对称密码体制最大的区别。

加密模型:

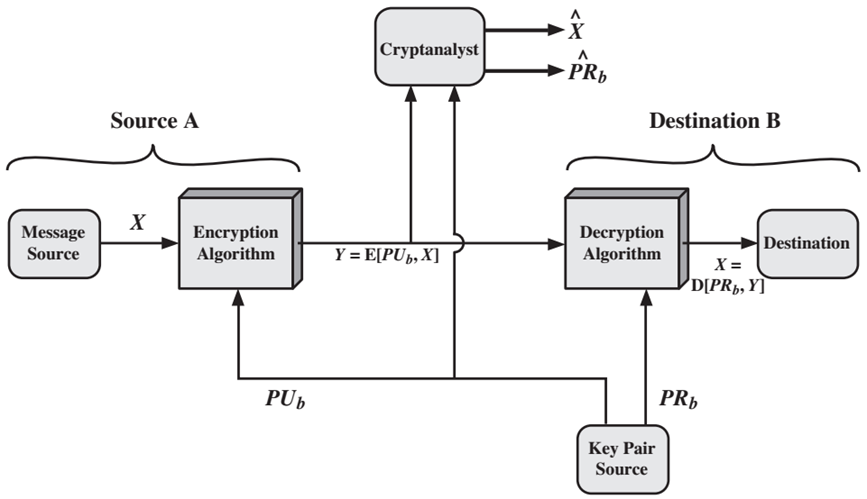
15507319938201550731993820

认证模型:

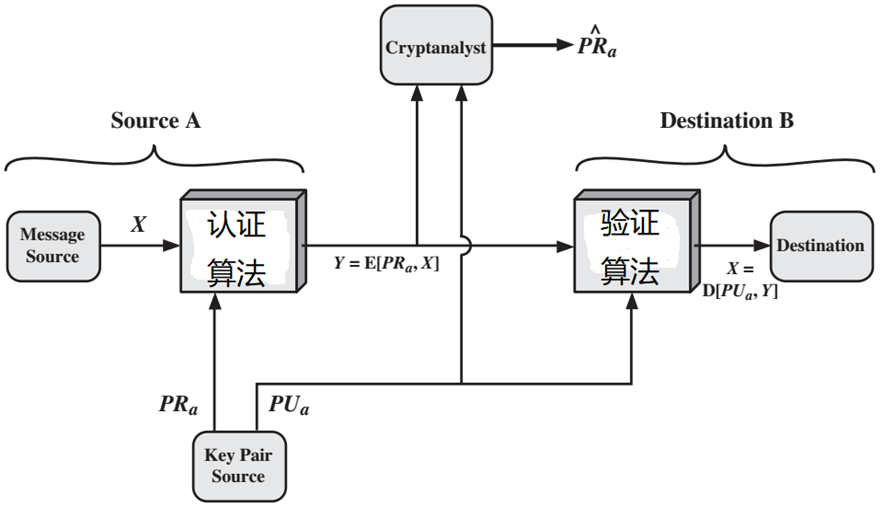
15507320360321550732036032

加密认证模型:

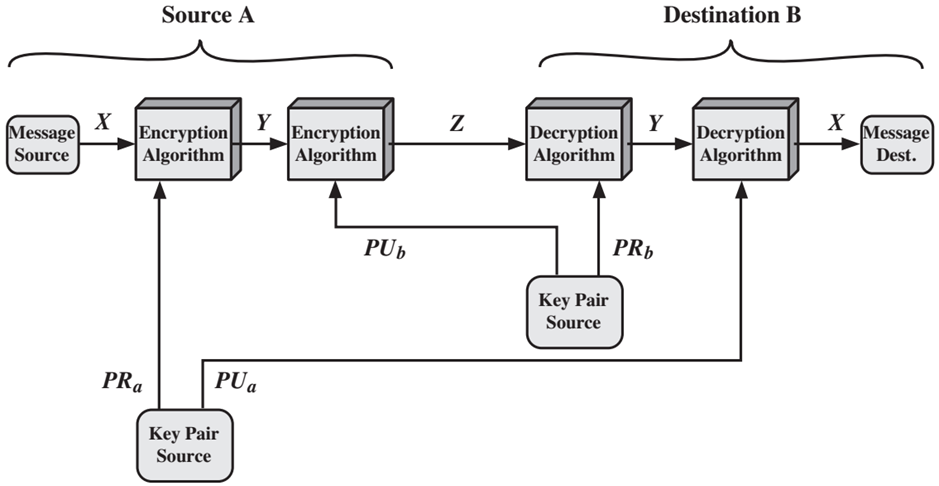
15507320493381550732049338

对公钥密码的要求

  1. 接收方B产生密钥对（公钥PKB和私钥SKB）在计算上是容易的。
  2. 发方A用收方的公钥对消息m加密产生密文c，即c=EPKB[m]在计算上是容易的。
  3. 收方B用自己的秘密钥对c解密，即m=DSKB[c]在计算上是容易的。
  4. 敌手由B的公钥PKB求私钥SKB在计算上是不可行的。
  5. 敌手由密文c和B的公钥PKB恢复明文m在计算上是不可行的。

要满足上述条件即是要找一个陷门单向函数。

  • 单向函数：两个集合X、Y之间的一个映射，使得由x∈X易于计算它的像y=f(x)∈Y，由y计算它的原像x是不可行的。
  • 易于计算：指函数值能在其输入长度的多项式时间内求出，即如果输入长n比特，则求函数值的计算时间是na的某个倍数，其中a是一固定的常数。这时称求函数值的算法属于多项式类P，否则就是不可行的。
  • 陷门单向函数：指该函数是易于计算的，但求它的逆是不可行的，除非再已知某些附加信息。当附加信息给定后，求逆可在多项式时间完成。

陷门单向函数是一族可逆函数fk，满足

  1. 当已知k和X：Y=fk(X)易于计算
  2. 当已知k和Y：X=f-1k(Y)易于计算
  3. 当已知Y但未知k：X=f-1k(Y)计算上是不可行的

RSA算法

算法描述

1. 密钥的产生

•选两个大素数p和q；（保密）

•计算n=p×q, ϕ(n)=(p−1)×(q−1); （n公开，ϕ(n)保密）

•随机选一整数e∈(1, ϕ(n))，满足：

gcd(ϕ(n), e) =1（公钥e）

•计算d，满足：d×e ≡ 1 (mod ϕ(n))（私钥d）

2. 加密

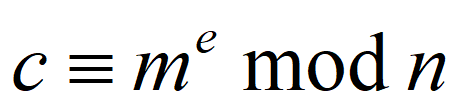
15507324079661550732407966

3. 解密

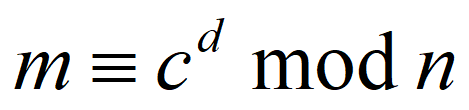
15507324123281550732412328

第10章 密钥管理和其他公钥密码体制

Diffie-Hellman密钥交换

Diffie和Hellman于1976年提出，许多商业产品都使用了这种密钥交换技术。

算法描述

  1. 用户A随机选择一个私有的大整数xA<q，计算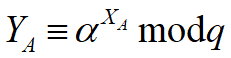15507325894781550732589478，并将结果传送给用户B；
  2. 用户B随机选择一个私有的大整数xB<q，计算 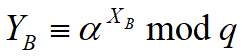15507325967861550732596786 ，并将结果传送给用户A；

​ 3）用户A计算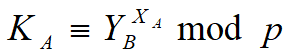：15507325629681550732562968

​ 4）用户B计算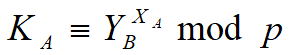：15507325659111550732565911

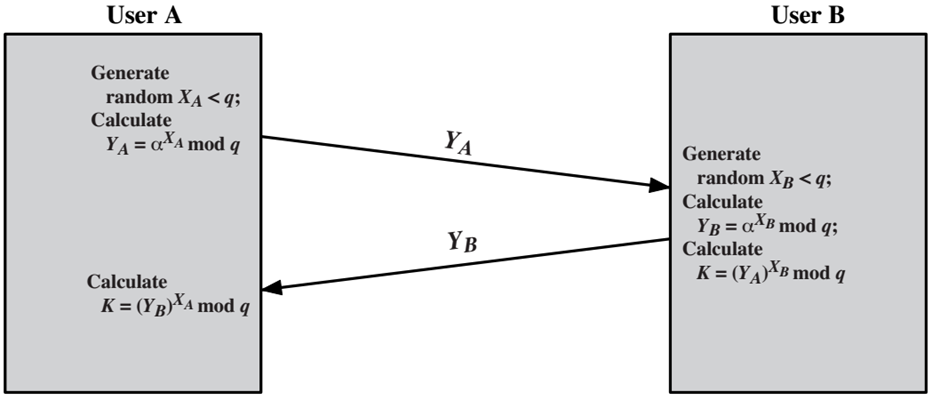
15507326199681550732619968

中间人攻击

  • 用户A将YA发送给B的过程中，中间人D截取YA，并用自己的YD取代YA发送给用户B。
  • 用户B将YB发送给A的过程中，中间人D截取YB，并用自己的yD取代YB发送给A。
  • A、B和D三者分别计算会话密钥：

​ A与D共享会话密钥KA：

​ B与D共享会话密钥KB：

​ 一般情况下KA ≠ KB ，但A与B对此一无所知。

ElGamal密码体制

ElGamal密码体制是ElGamal于1984年提出，除了RSA密码体制之外著名的公钥密码体制之一。安全性基于离散对数问题的困难性。

ElGamal算法

(1) 参数定义和密钥生成

  • 选取大素数p，g∈Zp*是一个本原元素（生成元）。
  • p，g为系统中所有用户共享。
  • 系统中每个用户U都随机挑选一个整数xU，1≤ xU ≤ p−1，并计算：

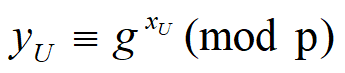
15507327625331550732762533

​ 用户U的公钥为yU，私钥为xU。

(2) 加密算法

  • A选择一个随机数r∈[2，p-2]并计算：

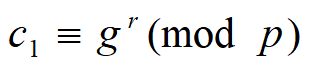
15507328281121550732828112

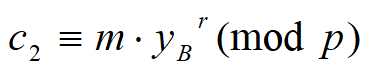
15507328322641550732832264

(3) 解密算法

  • B接收到密文(c1，c2)后，计算：

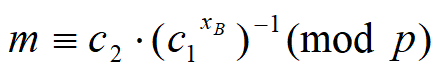
15507328841691550732884169

椭圆曲线密码学

椭圆曲线密码体制（Elliptic Curve Cryptography，ECC）：

  • 利用有限域上椭圆曲线的点集构成的群实现。
  • 安全性基于椭圆曲线上求离散对数问题的困难性。
  • 由于椭圆曲线密码体制具有计算量小，处理速度快、存储空间占用小、带宽要求低等优点，在电子商务、电子政务等应用领域得到广泛关注。

定义

椭圆曲线主要有：

  • 实数域上的椭圆曲线
  • 有限域GF(p)上的椭圆曲线
  • 有限域GF(2m)上的椭圆曲线

不同数域上的椭圆曲线的表示形式不一样，甚至其上的运算也不一样。

椭圆曲线上的密码体制（ECC）：有限域椭圆曲线上的任意两个点相加，结果仍然是曲线上的点。

  • 所有点都落在某一个区域内，组成一个有限Abel群，与密码长度相对应。
  • 密码长度越长，这个区域就越大，安全层次就越高，但计算机速度越慢，反之亦然。
  • 椭圆曲线密码体制的安全性在于椭圆曲线点群上的离散对数问题的困难性。
  • 已知椭圆曲线Ep(a, b)和点G，随机生成一个整数d，容易计算Q=d×G，但给定Q和G计算d就相对困难。

椭圆曲线密码的安全性

ECC在理论上和实践上都取得了很大的进展，它是代替RSA公钥密码体制最强有力的竞争者。与RSA算法相比，ECC有以下的优点：

  • ECC使用的密钥比RSA中使用的密钥要短得多。
  • 密钥长度相同时，ECC与RSA所需的计算量差不多。

因此，与具有同等安全性的RSA相比，由于ECC使用的密钥更短，所以ECC所需的计算量比RSA少。

第11章 Hash函数

完整性（Integrity）：指信息在存储或传输过程中保持未经授权不能改变的特性。

Hash函数

Hash函数把任意长度的输入，通过算法变换成固定长度的输出，该输出就是Hash值或消息摘要（Message Digest）。

设H：X→Y是一个Hash函数，X表示所有消息的集合（有限集或无限集），Y表示所有消息摘要构成的有限集合。

Hash函数H具有单向性：

  • 从x计算y=H(x)是容易的
  • 从y=H(x)计算x是困难的

对于Hash函数的安全要求，通常采用下面的三个问题来进行判断：

  1. 已知y∈Y，寻找x∈X，使得H(x)=y。
  2. 已知x∈X，寻找x’∈X，使得x’≠x，并且H(x’)=H(x)。
  3. 寻找x，x’∈X，使得x’≠x，并且H(x’)=H(x)。

如果一个Hash函数对这三个问题都是难解的，即计算上不可行，则认为它是安全的。

如果有两个消息x，x’∈X，x’≠x，且H(x’)=H(x)，我们就说这两个消息是碰撞消息。

  • 单向：第(1)个问题不可解。
  • 抗弱碰撞：第(1)和(2)问题不可解。
  • 抗强碰撞：第(1)和(3)问题不可解。

Hash函数的构造方法

构造Hash函数的方法主要有：

  • 基于公钥密码的构造方法
  • 基于分组密码的构造方法
  • 直接构造法

1. 基于公钥密码的构造方法

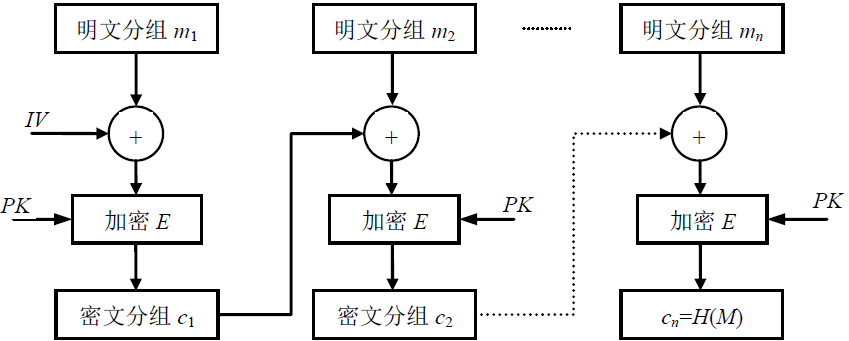
​ 设明文M=m1m2…mn，以公钥密码体制为基础，使用公钥PK及初始变量IV，通过密文分组链接（CBC）模式对消息分组进行加密，得到密文分组。将输出的最后一个密文分组c**n**作为Hash函数的输出值H(M)。

15507337931871550733793187

2. 基于分组密码的构造方法

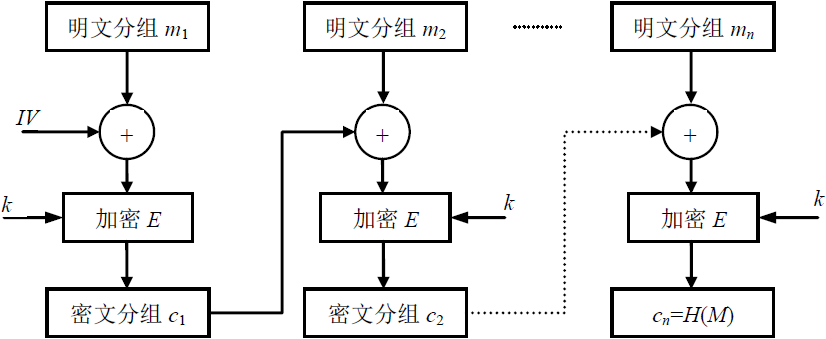
​ 设明文M=m1m2…mn，使用CBC模式，输入初始变量IV和对称密钥k，对消息分组进行加密，得到密文分组。将输出的最后一个密文分组c**n**作为Hash函数的输出值H(M)。

15507338035781550733803578

3. 直接构造Hash函数

​ 这类Hash函数并不基于任何假设和密码体制，它是通过直接构造复杂的非线性关系达到单向性要求来设计单向Hash函数。这类Hash函数典型的有：MD4、MD5、SHA-1、SHA-256等算法。

MD5算法

MD5（Message-Digest Algorithm 5）算法由Rivest在1991年提出的一种Hash函数，经MD2、MD3和MD4发展而来。

MD5算法描述

MD5算法采用迭代型Hash函数的一般结构：

•算法的输入为任意长的消息M。

•M分为512 bit长的块，每个块又划分为十六个32 bit的子块。

•算法的输出是由四个32 bit的块组成，将它们级联成一个128 bit的消息摘要。

算法步骤

(1) 消息填充

​ 对X bit长的消息填充：

•使填充后的消息bit长度X1≡448 (mod 512)，即填充后的消息长度为512bit的某一倍数减64bit，留出的64bit备第(2)步使用。

•填充方式是固定的，即第1位为1，其后各位皆为0。

•如果消息长度X为448bit，仍需填充512bit，使其长度变为960bit，因此填充的bit数大于等于1而小于等于512

(2) 附加上消息的长度值

​ 用步骤(1)留出的64bit以Little-endian方式来表示消息被填充前的长度值。

•如果消息长度大于264，则以264为模数取模，即64bit存放的是X (mod 264)的二进制表示值。

•Little-endian方式是指数据的低位有效字节（或有效位）存于低地址字节（或位），高位有效字节（或有效位）存于高地址字节（或位）。

​ 用步骤(1)留出的64bit以Little-endian方式来表示消息被填充前的长度值。

​ 前两步执行完后，消息的长度为512bit的倍数（设为L倍），则可将消息划分为L个长度为512bit的块m0, m1, …, mL-1，而每一块又可划分为16个32bit长的子块。

(3) 缓冲区初始化

​ 算法使用了128bit长的缓冲区以存储中间结果和最终的消息摘要，缓冲区可表示为4个32bit长的寄存器A、B、C、D，每个寄存器都以Little-endian方式存储数据，其初值（用十六进制表示）取为：

​ A = 01234567

​ B = 89abcdef

​ C = fedcba98

​ D = 76543210

(4) 压缩函数处理

​ 以块为单位对消息进行处理，每一消息块mj（j = 0, …, L-1）都经一压缩函数HMD5处理。压缩函数有4轮处理过程，每一轮由16步迭代组成。

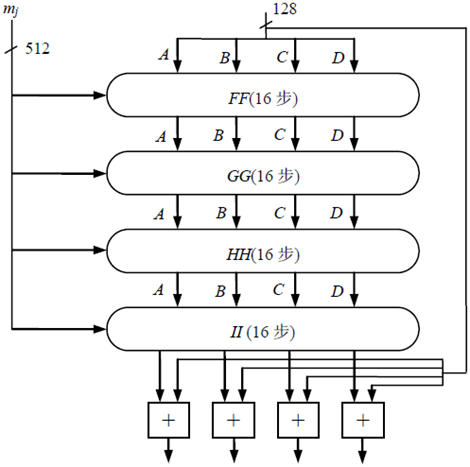
15507339976711550733997671

(5) 输出消息摘要

​ L个消息块mj（j = 0, …, L-1）都被处理完后，最后一个压缩函数的输出即为产生的128bit消息摘要。

压缩函数的处理过程

压缩函数HMD5的4轮处理过程相似，分别用逻辑函数FF、GG、HH、II表示，它们分别为是

  • FF (A, B, C, D, M[k], S, T[i])
  • GG(A, B, C, D, M[k], S, T[i])
  • HH(A, B, C, D, M[k], S, T[i])
  • II (A, B, C, D, M[k], S, T[i])

的缩写。

​ 每轮的输入为当前处理的消息块mi和缓冲区的当前值A、B、C、D，输出仍放在缓冲区中以产生新的A、B、C、D。经过4轮运算，第4轮的输出再与第1轮的输入按模232相加，相加的结果即为压缩函数HMD5的输出。

MD5算法的安全性

目前对MD5的攻击已取得以下结果：

​ (1) 对单轮的MD5，使用差分密码分析可在合理的时间内找出具有相同Hash值的两个消息。但这种攻击还未能成功地推广到4轮MD5。

​ (2) 可找出一个消息块和两个相关的缓冲区变量ABCD的不同输入值，MD5对单个512bit消息块的运算得到相同的输出。目前这种攻击还未能成功地推广到整个算法。

​ (3) 对单个512bit长的消息块已成功地找出了碰撞，即可找出另一个消息块，使得经过MD5运算，两个消息块的输出Hash值相同。目前这种攻击还未成功推广到一个具有初值IV的整个消息上。

SHA-1算法

SHA（Secure Hash Algorithm）算法由美国国家标准和技术协会（NIST）提出，并作为联邦信息处理标准（FIPS PUB 180）在1993年公布。

两年之后，SHA-1，第一个SHA的后继者发布了。为了提升输出的范围和变更一些细微设计，另外还有四种变体曾经发布：SHA-224, SHA-256，SHA-384 和SHA-512（这些也称作SHA-2）。

这里介绍SHA-1算法，其结构与MD5非常类似：

  • 输入消息的最大长度不超过264 bit
  • 输入消息按照512 bit的块进行处理
  • 产生160 bit的消息摘要

SHA-1算法描述

​ (1) 消息填充

​ 消息填充过程与MD5的步骤(1)相同，设输入的消息为M，X≤264-1表示消息的长度。

•使填充后的消息长度X1≡448 (mod 512)，即填充后的消息长度为512bit的某一倍数减64bit，留出的64bit备第(2)步使用。

•填充方式是第1位为1，其后各位皆为0。

•如果消息长度X=448bit，仍需填充512bit，使其长度变为960bit，因此填充位数是1~512比特。

​ (2) 附加上消息的长度值

​ 用步骤(1)留出的64比特以Big-endian方式来表示消息被填充前的长度值，即64比特存放的是消息长度X的二进制表示值。

​ 前两步执行完后，消息的长度为512的倍数（设为L），将消息划分为L个长度为512bit的块m0，m1，…，mL-1，每一块又可划分为16个32比特长的子块。

​ (3) 缓冲区初始化

​ 算法使用了160bit长的缓冲区以存储中间结果和最终的消息摘要，缓冲区可表示为5个32比特长的寄存器A、B、C、D、E。每个寄存器都以Big-endian方式存储数据，其初值（用十六进制表示）取为

​ A=67452301 B=efcdab89

​ C=98badcfe D=10325476

​ E=c3d2e1f0

​ (4) 压缩函数处理

​ 以块为单位对消息进行处理，每一消息块mj（j=0, …, L-1）都经一压缩函数HSHA处理。压缩函数有4轮处理过程，每一轮由20步迭代组成。

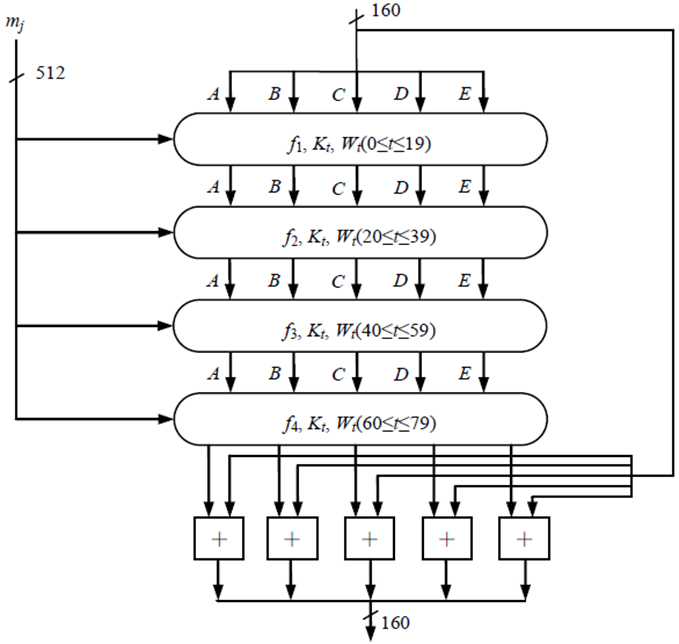
15507343462171550734346217

​ (5) 输出消息摘要

​ L个消息块mj（j=0,…,L-1）都被处理完后，最后一个分组的输出即为160比特的消息摘要。

MD5与SHA-1的比较

​ 两种算法相似点在于：

  1. 结构类似：都是以MD4为基础设计的。
  2. 算法描述起来都较为简单：实现起来也较为简单，均不需要较大的程序和代换表。

​ 两种算法不同点在于：

  1. 抗攻击的强度：SHA-1抗穷举攻击的强度高于MD5抗穷举攻击的强度。
  2. 速度和效率：在相同硬件上实现时，SHA-1的速度要比MD5的速度慢，MD5的执行效率比SHA-1高。
  3. 数据的存储方式：MD5使用Little-endian方式，SHA-1使用Big-endian方式。

Hash函数的攻击

​ 假设攻击者知道Hash算法，攻击者的主要目标：

  • 寻找具有给定消息摘要的一对或多对碰撞消息。
  • 寻找具有相同消息摘要的一对或多对碰撞消息。

评价Hash函数的好坏最简单的方法是看攻击者找到一对碰撞消息所花的代价有多大。

​ 1. 生日问题

​ 生日攻击来自于概率论中的生日问题：在一个教室中至少要有k个学生才能够使得有两个学生生日相同的概率大于1/2，求k值至少多大？

​ P(n, k)：n种取法，共取k次，发生碰撞的概率。则生日问题可记为P(365, k)≥1/2，则k为多少？

  • k=23：P(365, 23)=0.5073
  • k=100：P(365, 100)=0.9999997

​ 2. 寻找具有相同输出摘要的碰撞消息

​ 已知Hash函数有n个可能的输出摘要，特别地，如果输出摘要为m比特长，即可能的输出摘要个数n=2m，若Hash函数k个随机输入消息中至少有两个产生相同输出的概率大于1/2，求k值至少多大。

​ 生日攻击意味着要保证消息摘要对碰撞问题是安全的，消息摘要的长度应该有一个下界。

  • 例如，长度为40比特的消息摘要是非常不安全的，因为仅仅220个随机Hash函数值中就有1/2的概率发生一次碰撞。
  • 对于安全的消息摘要，现在实际使用的消息摘要一般为160比特或者更长。